Optimizing Unique Paths LeetCode Problem

Unique Paths

There is a robot on an m x n grid. The robot is initially located at the top-left corner (i.e., grid[0][0]). The robot tries to move to the bottom-right corner (i.e., grid[m - 1][n - 1]). The robot can only move either down or right at any point in time.

Given the two integers m and n, return the number of possible unique paths that the robot can take to reach the bottom-right corner.

Problem can be found here: https://leetcode.com/problems/unique-paths/description/

Disclaimer: This post considers that you already have a knowledge on Dynamic Programming, which is a technique, by which we can find solution of a bigger problem by solving smaller parts of it. Please have a look at this playlist which helped me a lot in learning DP.

Test Cases

Input: m = 3, n = 2

Output: 3

Explanation: From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:

1. Right -> Down -> Down
2. Down -> Down -> Right
3. Down -> Right -> Down

Intuition

Dynamic programming would work here, as we need to find all possible path combinations. We should be thinking, in how many possible way we reach a single cell, don’t forget that we have only two possible moves, which is right and down.

Lets consider a 3x3 matrix,

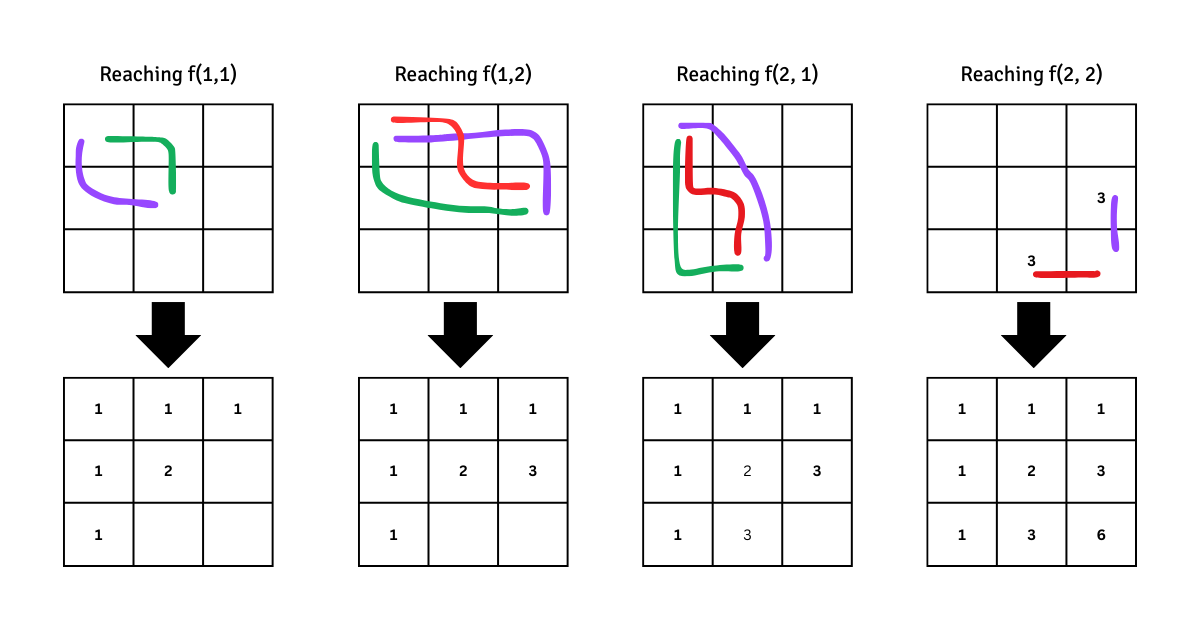
For grid[0][0], its the start of they cell, we can consider it to be one way.

For grid[0][1], there is only one possible way, which is from grid[0][0].

For grid[1][0], there is only one possible way, which is from grid[0][0].

For grid[1][1], we have two possible way here, one from grid[1][0] and another from grid[0][1].

Similarly,

For grid[0][2] and grid[2][0], we have only one possible way.

For grid[1][2] and grid[2][1], we have 3 possible way from the start.

Finally for grid[3][3], we have 6 possible way from the start.

Did you find the repeatition, yeah, we just need to sum the left cell and the top cell of the current cell, which gives us f(i, j) = f(i-1, j) + f(i, j-1).

This can be also be solved with mathematical approach using permutation. But we would be using Dynamic programming approach and would be optimizing it.

Approach

This bring me back to the old Math days, where we need to describe the problem with sentence.

Here f(i, j) will give us number of possible ways it can be reached fromm f(0, 0).

We should have a base case which is f(0, 0) is 1. Using that, we would be building our solution up.

We can find, f(i, j) using f(i-1, j) + f(i, j-1). But for first row and first column, we don’t have previous cell to add up. We might need to change the function a bit for such scenarios.

And the solution would be at f(m-1, n-1), where m is the number of rows and n is the number of columns.

class Solution {
    public int uniquePaths(int m, int n) {
        int[][] dp = new int[m][n];
        dp[0][0] = 1;
        for(int i = 0; i < m; i++) {
            for(int j = 0; j < n; j++) {
                if(j > 0 && i > 0) {
                    dp[i][j] = dp[i-1][j] + dp[i][j-1];
                } else if(j > 0) {
                    dp[i][j] = dp[i][j-1];
                } else if(i > 0) {
                    dp[i][j] = dp[i-1][j];
                }
            }
        }
        return dp[m - 1][n - 1];
    }
}

Complexity

Time Complexity: O(N^2)

Space Complexity: O(N^2)

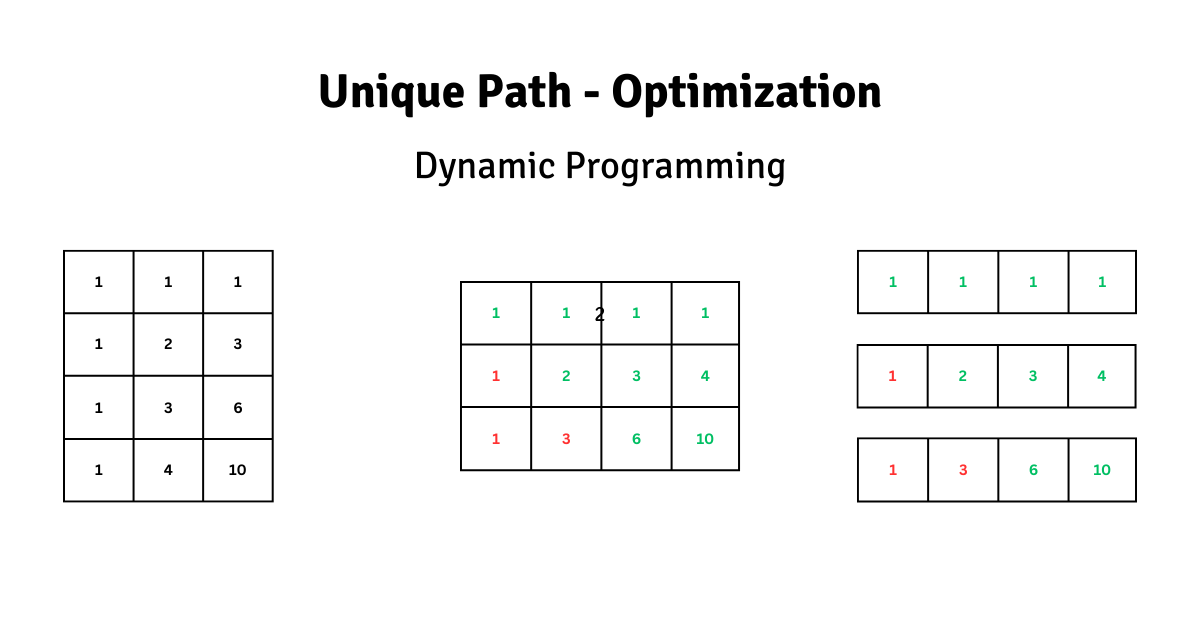
Optimized Approach

You can find that there is redundant data on the top and bottom of the diagonal, which can be avoided. And when i == j, the value is just double of the upper cell, for the remaining cells it can be calculate by adding the right and top cells. Just forming a upper triangular matrix.

This can further be optimized by using 1D array, and updating the same cell, instead of going 2D.

class Solution {
    public int uniquePaths(int m, int n) {
        int row = Math.min(m, n);
        int column = Math.max(m, n);
        int[] dp = new int[column];
        for(int i = 0; i < column; i++) {
            dp[i] = 1;
        }
        for(int i = 1; i < row; i++) {
            for(int j = i; j < column; j++) {
                if(i == j) {
                    dp[i] = 2 * dp[i];
                } else {
                    dp[j] = dp[j-1] + dp[j];
                }
            }
        }
        return dp[column - 1];
    }
}

Complexity

Time Complexity: O(N^2)

Space Complexity: O(N)